Intervention de Jason Ross, responsable de The LaRouche Organization (TLO), lors de la conférence organisée par S&P et l’Institut Schiller à Paris, les 8 et 9 novembre 2025.
La raison créatrice est un principe fondamental de l’univers ! L’univers répond à nos idées en nous accordant un pouvoir accru. Nos pensées peuvent déplacer des montagnes. Je souhaiterais ajouter un commentaire aux propos de l’intervenant précédant (Sébastien Drochon) concernant la réfutation polémique de Bertrand Russell et David Hilbert par Kurt Gödel. La brillante démonstration de Gödel repose sur la nature intrinsèquement autoréférentielle de la raison. L’esprit regarde à la fois en lui-même et autour de lui.
Bertrand Russell a tenté de créer un système logique où aucun système ne pourrait jamais se référer à lui-même. Ceci permettrait d’éviter les énoncés indécidables simples comme « Cet énoncé est faux ». Mais Gödel a contourné les défenses de Russell et créé un moyen permettant à un énoncé de se référer à lui-même. Ce faisant, il a formulé un énoncé que la raison humaine peut savoir être vrai, mais que la logique ne peut prouver.
Adoptons une approche inverse à celle de Russell et Hilbert. Nous ne recherchons pas un système logique capable d’exprimer toutes les vérités, mais plutôt une approche de la découverte empreinte de vérité et d’introspection, qui transcende toute logique. Prenons quelques exemples, tirés des domaines de l’économie, de la géométrie et des mathématiques.
Changement économique non quantitatif et illogique
L’histoire économique humaine est caractérisée par des révolutions fondamentales dans notre rapport aux matériaux et à une sorte de « feu » généralisé — les transformations que nous utilisons pour alimenter notre activité économique.
Nous allons examiner quatre domaines :
- le feu de bois,
- la chimie,
- l’électricité,
- le nucléaire.
Grâce au bois, nous pouvons nous protéger des animaux, cuire les aliments en évitant les parasites toxiques, améliorer nos matériaux, défricher les terres et chauffer les bâtiments.
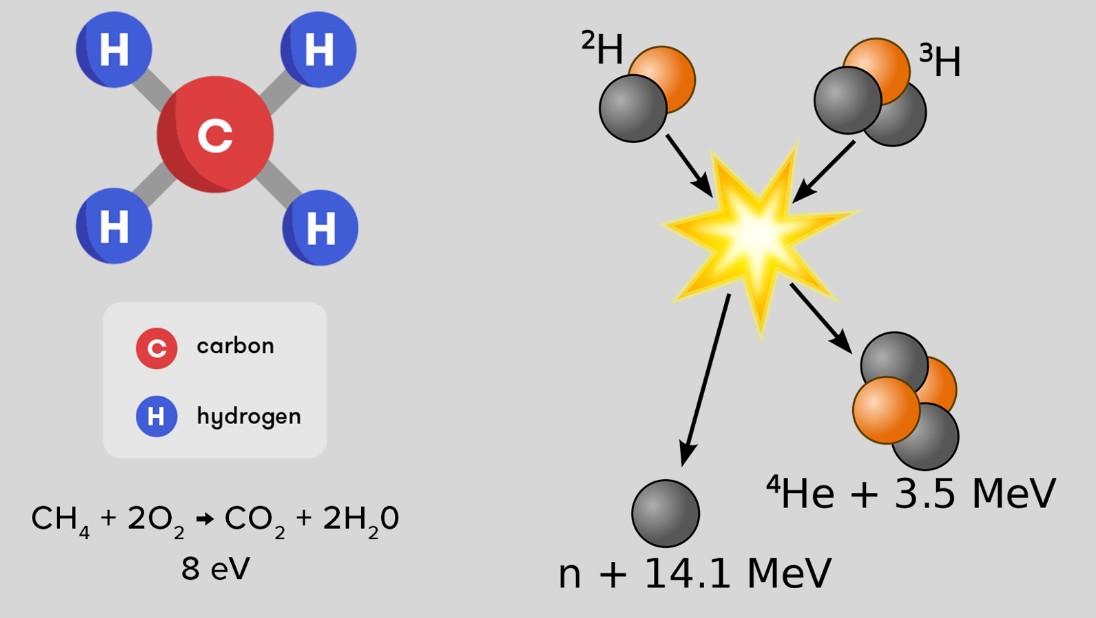
Le charbon de bois représente une forme d’énergie supérieure. Sa combustion, plus chaude et plus propre, est suffisamment intense pour réduire les minerais et en libérer le métal.
La transformation d’une roche en métal brillant n’était absolument pas une attente logique pour les civilisations anciennes. En réalité, cela semble insensé. C’est une découverte.
Le monde de la chimie nous ouvre les portes d’une puissance nouvelle et d’un langage inédit. Les roches possèdent une couleur, une dureté et une densité. Mais les éléments et les réactions chimiques sont caractérisés par des valences et des enthalpies.
Il est impossible de décrire logiquement les transformations chimiques avec le langage utilisé avant Antoine Lavoisier et Dmitri Mendeleïev. Un élément de son tableau n’a ni couleur, ni dureté, ni densité. Prenons l’exemple du charbon et du diamant, tous deux composés exclusivement de carbone.
En exploitant l’énergie sous forme d’électricité, nous nous affranchissons des seuls rejets thermiques et chimiques des combustibles. Les moteurs chimiques peuvent produire du mouvement, mais en le convertissant en électricité, nous pouvons le transmettre par des câbles, utiliser des moteurs pour un meilleur contrôle des machines, et nous disposons de lasers, de la soudure électrique et d’ordinateurs. Quelle que soit la quantité de mouvement ou de chaleur produite auparavant, rien ne peut égaler les possibilités offertes par l’électricité. Il s’agit d’une économie fondamentalement nouvelle, dont la valeur ne se mesure pas à l’aune de ce qui a existé auparavant.
Enfin, le « feu » nucléaire exploite l’incroyable énergie du noyau atomique, dont le potentiel énergétique est un million de fois supérieur à celui des réactions chimiques. Lorsque les lois de la thermodynamique ont été établies au XIXe siècle, l’énergie nucléaire était inconnue. À quel point la première loi de la thermodynamique est-elle incomplète, puisqu’elle ignorait tout un pan de l’énergie ? Grâce à l’énergie nucléaire, nous pourrions contrôler les confins de notre système solaire et dévier la trajectoire des astéroïdes et comètes dangereux.
Parallèles avec les mathématiques

Parlons maintenant plus en détail du rôle joué par Georg Cantor et Bernhard Riemann dans les percées économiques de Lyndon LaRouche.
Commençons par examiner les classes de nombres, en parallèle avec les formes de « feu » que nous venons d’évoquer.
Les nombres entiers sont les nombres naturels : 1, 2, 3, 4. Ils nous indiquent combien de vaches nous avons, combien de céréales nous avons.
Les nombres entiers comprennent les nombres entiers négatifs, qui ont été rejetés pendant des centaines d’années avant d’être acceptés comme faisant partie de la famille des nombres.
Les nombres rationnels sont des rapports, c’est-à-dire des fractions. Un et demi, sept cinquièmes, sont des nombres compris entre les nombres entiers.
Les nombres irrationnels ne peuvent absolument pas être exprimés par une fraction. L’exemple le plus célèbre est celui du doublement du carré.
Nous cherchons à construire un carré dont l’aire soit le double de celle d’un carré donné. Comment y parvenir ? La réponse se trouve dans le Ménon, un des dialogues de Platon. Ce problème est si complexe qu’il est désigné par un symbole nouveau : la racine carrée de deux.
Réfléchissez à ce terme : c’est la racine d’un carré de deux. Quelle est la racine d’un carré ? Son côté. Le « côté du carré de 2 » ne peut être exprimé sous forme de fraction, mais il peut être construit géométriquement.
Il y a ensuite les nombres transcendants, qui ne peuvent être exprimés par aucune relation algébrique. Les deux plus célèbres sont pi, qui exprime la relation entre la courbe et la droite, entre le carré et le cercle, fondamentalement différents selon Nicolas de Cues. Le second est e, la base des logarithmes naturels, un nombre qui incarne la croissance autoréférentielle elle-même.
Cette série de percées, qui consiste à étendre le domaine des nombres, est parallèle aux transformations économiques.
Bernhard Riemann

Dans son article sur les fonctions nommées d’après Niels Abel, Riemann a exprimé une relation entre l’obtention de fonctions transcendantales supérieures et un changement fondamental de topologie.
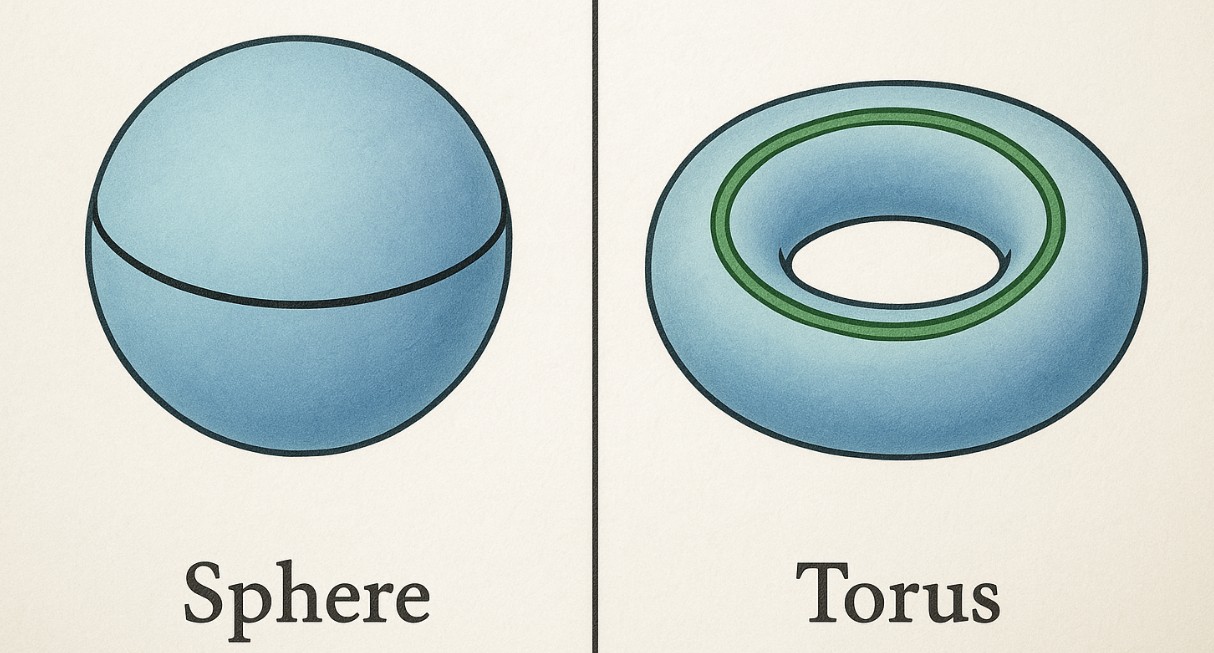
Prenons l’exemple d’une sphère. Si vous tracez une courbe fermée sur la sphère, vous la couperez en deux morceaux.
Mais existe-t-il des formes dans lesquelles on peut découper une courbe sans qu’elles se séparent en deux morceaux ? Pouvez-vous en citer quelques-unes ?
Le tore possède un degré de connectivité supérieur à celui de la sphère. On peut le découper selon sa circonférence, et il se déplie pour former une autre forme de cylindre. On peut également le découper selon sa section circulaire, ce qui nous donne aussi un cylindre. Or, toute découpe du cylindre le divise en deux.
Alors, quelle est la différence entre la sphère et le tore ? Existe-t-elle quelque part ? Peut-on la localiser d’une manière ou d’une autre ?
Prenons l’exemple d’une découverte scientifique. Quels en sont les effets économiques et civilisationnels ? Une découverte naît dans un esprit, à un endroit donné, mais elle a pour effet de transformer fondamentalement la civilisation humaine.
Voilà la valeur économique !
Georg Cantor

Y a-t-il quelque chose de plus grand que l’infini ? Existe-t-il différentes sortes d’infini ? C’est une question à laquelle Georg Cantor a répondu en démontrant que l’infini continu des nombres réels (y compris les irrationnels et les transcendants évoqués précédemment) est fondamentalement plus grand que l’infini des nombres naturels.
Réfléchissez-y en termes économiques :
À l’âge du bronze, le potentiel économique et culturel de l’espèce humaine était-il infini ? Existait-il un nombre précis d’activités différentes que la société pouvait entreprendre ? 1427 ? Non, il n’y a pas de limite ; c’est infini !
Oui, aujourd’hui, notre champ d’action potentiel est bien plus vaste. Nous vivons dans un infini supérieur !
L’évolution humaine se manifeste par la création de « plus que » plutôt que de « plus de ».
Puisque nos découvertes sont toujours dénombrables et que l’univers réel est continu, nous n’en finirons jamais de tout découvrir, même si la civilisation humaine se poursuit éternellement !
Une perspective passionnante ! Un univers magnifique !
Où aller ?
À quoi ressemble aujourd’hui un monde où l’on privilégie le « plus que » au « plus de » ? Quelle voie emprunterons-nous à partir de maintenant ?
L’intervenant suivant (Benoit Odille) vous en donnera une idée.